Angles Of Of And Interior Polygon A Sum Exterior

Interior And Exterior Angles Of A Polygon Dummies

Polygon exterior angle sum theorem if a polygon is convex, then the sum of the measures of the exterior angles, one at each vertex, is 360 . consider the sum of the measures of the exterior angles for an n -gon. the sum of the measures of the exterior angles is the difference between the sum of measures of the linear pairs and the sum of measures of the interior angles. The sum of the exterior angles of any polygon is 360 degrees. the formula. tells you the sum of the interior angles of a polygon, where n represents the number of sides. practice questions. use your knowledge of the sums of the interior and exterior angles of a polygon to answer the following questions. solve for x. Exterioranglessum of polygons. an exterior angle of a polygon is made by extending only one of its sides, in the outward direction. the angle next to an interior angle, formed by extending the side of the polygon, is the exterior angle. hence, we can say, if a polygon is convex, then the sum of the degree measures of the exterior angles, one. See more videos for sum of exterior and interior angles of a polygon.

Interior Angles Exterior Angles And The Sum Polygon Worksheets

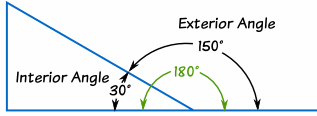
Interior angle + adjacent exterior angle = 180 degrees. in fact, the sum of (the interior angle plus the exterior angle) of any polygon always add up to 180 degrees. this is so because when you extend any side of a polygon, what you are really doing is extending a straight line and a straight line is always equal to 180 degrees. The sum of the measures of the interior angles of a polygon with n sides is (n 2)180.. the measure of each interior angle of an equiangular n-gon is. if you count one exterior angle at each vertex, the sum of the measures of the exterior angles of a polygon is always 360.

The sum of the exterior angles at each vertex of a polygon measures 360 o. divide 360 by the number of sides, to figure out the size of each exterior angle in this unit of regular polygons pdf worksheets for 8th grade and high school students. find the indicated interior angles algebra in polygons. Investigate the sum of exterior angles in polygons. sum of the exterior angles of a convex polygon. angle measures in polygons. sum of interior angles of polygones. Sum of all the interior angles of a polygon is equal to the product of a straight angle and two less than the number of sides of the polygon. in a regular polygon, all the interior angles measure the same and hence can be obtained by dividing the sum of the interior angles by the number of sides. sum of interior angles = (p 2) 180. Sal demonstrates how the the sum of the exterior angles of a convex polygon is 360 degrees. sum of interior angles of a polygon. sum of the exterior angles of a polygon. this is the currently selected item. practice: angles of a polygon. next lesson. geometric solids (3d shapes).

Angles In Polygons Geogebra

See full list angles of of and interior polygon a sum exterior on onlinemath4all. com. Exteriorangle of regular polygons. the sum of the exterior angles at each vertex of a polygon measures 360 o. divide 360 by the number of sides, to figure out the size of each exterior angle in this unit of regular polygons pdf worksheets for 8th grade and high school students. In fact, the sum of ( the interior angle plus the exterior angle ) of any polygon always add up to 180 degrees. this is so because when you extend any side of a polygon, what you are really doing is extending a straight line and a straight line is always equal to 180 degrees.

Sum Of The Exterior Angles Of A Polygon Video Khan Academy

Students also learn the following formulas related to convex polygons. the sum of the measures of the interior angles of a polygon is always 180(n-2) degrees, where n represents the number of sides of the polygon. the sum of the measures of the exterior angles of a polygon is always 360 degrees. The sum of the measures of the exterior angles of a polygon, one at each vertex, is 360. measure of a single exterior angle formula to find 1 angle of a regular convex polygon of n sides = 1 + 2 + 3 = 360 . More sum of exterior and interior angles of a polygon images.

Sum of angles in a triangle. you can do this. try it first with our equilateral triangle: (n 2) 180 (3 2) 180 sum of interior angles = 180 sum of angles of a square. and again, angles of of and interior polygon a sum exterior try it for the square:.

Regular polygon : a regular polygonhas sides of equal length, and all its interior and exterior angles are of same measure. irregular polygon : an irregular polygon angles of of and interior polygon a sum exterior can have sides of any length and angles of any measure. Interiorangleof a polygon = 180 exterior angle of a polygon. method 3: if we know the sum of all the interior angles of a regular polygon, we can obtain the interior angle by dividing the sum by the number of sides. interior angle = sum of the interior angles of a polygon / n. where n is the number of polygon sides. Although you know that sum of the exterior angles is 360, you can only use formula to find a single exterior angle if the polygon is regular! consider, for instance, the pentagon pictured below. even though we know that all the exterior angles add up to 360 , we can see, by just looking, that each $$ \angle a \text{ and } and \angle b $$ are. In a polygon, the measure of each interior angle is (5x+90) and ex terior angle is (3x-6) . how many sides does the polygon have? solution : in any polygon, the sum of an interior angle and its corresponding exterior angle is 180 . that is, interior angle + exterior angle = 180 (5x + 90) + (3x 6) = 180 .

The sum of the measures of the interior angles of a convex n-gon is (n 2) 180 the measure of each interior angle of a regular n-gon is. 1/n (n 2) 180 or [(n 2) 180] / n. the sum of the measures of the exterior angles of a convex polygon, one angle at each vertex is. 360 . Interior angle : an interior angle of a polygon is an angle inside the polygon at one of its vertices. exterior angle : an exterior angle of a polygon is an angle outside the polygon formed by one of its sides and the extension of an adjacent side. Since you are extending a side of the angles of of and interior polygon a sum exterior polygon, that exterior angle must necessarily be supplementary to the polygons interior angle. together, the adjacent interior and exterior angles will add to 180. for our equilateral triangle, the exterior angle of any vertex is 120. for a square, the exterior angle is 90.